Disclaimer: All of the information provided in this article is my personal opinion and is meant for entertainment and information purposes only. I am not a professional in the field but just a guy on the internet. Make sure you do your own research and consult with a professional such as a financial planner or a CPA before making investment decisions.
Assets vs Liabilities
Assets are things that generate money, while liabilities are things that take money away from you. Many of us aren’t always clear on what truly constitutes an asset. Can you rely on an asset to provide you income when you retire? Is your house an asset? Well, ask yourself: Is it generating income? If you’re living in the house and not renting out any rooms, it’s not producing income. In fact, it costs you money in the form of mortgage interest, property taxes, insurance, HOA fees, and maintenance costs just to live in it. While the value of the house may appreciate over time, you’ll only benefit from this growth when you sell the house. And if you sell your house and buy another one, you’re simply replacing one asset/expense with another. For that reason, I personally wouldn’t consider the home I live in to be an asset, as it won’t generate a steady stream of income in retirement.
The same logic applies to a car. Most people don’t use their car to generate income (e.g., driving for Uber). However, they still face costs like car payments, taxes, registration, insurance, gas, and maintenance. Generally, your personal car costs you money to operate and maintain, so I would consider it a liability. If you put money in a savings bank account, you receive interest payments each month, making it an asset. Similarly, stocks and bonds typically generate income through interest or dividend payments and/or appreciation in value over time. A business that generates profit is also considered an asset. Ultimately, you have the choice of where to allocate your money and which assets you want to invest in.
Investing
Investing, simply put, is the process of accumulating assets. Each asset comes with its own set of rules and is suited for different purposes. Every asset has its unique risks and rewards, with higher rewards typically demanding higher risks. From a financial perspective, a key question to ask when deciding what asset to invest in is: What is the return on investment (ROI)? In other words, what percentage of your invested money does this asset generate annually or monthly? For example, a 10% annual rate of return means that if you invest $5,000 in an asset, it would generate $500 (=$5,000 x 10/100) in returns after one year.
Another important question is how scalable the investment is. In a scalable investment, the return on investment doesn’t change based on the amount you invest—the same principles apply whether you invest $1,000 or $1 million. While scalability isn’t critical when you’re just starting out with $1,000, it becomes more important as your investments grow to $100,000 or even $1 million. If your strategy only works on a small scale, it may be difficult to replicate and could complicate your financial management as your net worth increases. For example, in a savings bank account, whether you have $1,000 or $1,000,000, you earn the same interest rate (your rate of return). Similarly, assets like stocks and bonds are scalable, and the principles of investing remain consistent whether you invest a small or large amount.
Compound Interest
Einstein famously said, “Compound interest is the eighth wonder of the world. He who understands it, earns it. He who doesn’t, pays it.” While many of us learn about compound interest in school, we often don’t grasp how powerful it is—perhaps because it’s not a straightforward or linear calculation. Let’s break it down with an example.
Suppose you invest $1,000 in an asset that offers a 10% annual return. The amount you initially invest is called the principal amount, denoted as P. The return on investment is the interest earned each year, denoted as R. At the end of one year, you would have your principal amount ($1,000) plus the interest it earned. The interest earned after one year is 10% of $1,000, or:
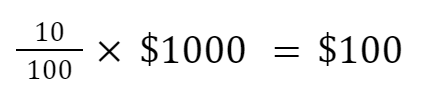
So, at the end of year one, your total would be $1,000 + $100 = $1,100. This is simple interest—you’re earning interest only on the principal.
Now, let’s consider what happens if you reinvest the interest for the second year. This means your interest will also earn interest, which is known as compounding or compound interest. In year two, your principal amount ($1,000) earns interest, and so does the $100 you earned in year one. So, after two years, the total will be:
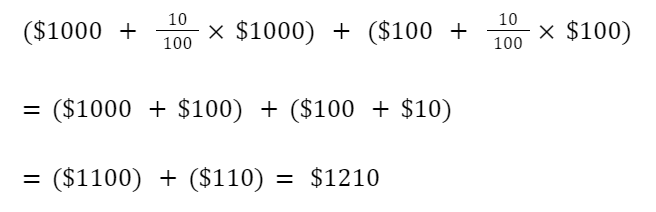
If you had not reinvested the interest, you would have earned another $100 in the second year, bringing your total to $1,200. However, with compound interest, you earned $1,210—an extra $10. While this may seem like a small gain, compounding adds up over time.
Let’s take a longer-term view. If you invest $1,000 for 10 years at a 10% annual return and reinvest the interest, your investment would grow to $2,593.74. Without reinvesting, you’d only have $2,000. Over 20 years, the difference grows to $3,727.50, and over 30 years, it becomes a whopping $13,449.40.
The mathematical formula for compound interest is shown as
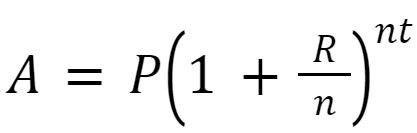
where,
A = the final amount,
P = Principal amount, or the beginning amount,
R = interest rate, or rate of return,
n = number of times the interest is applied for every period,
t = number of periods elapsed
The mathematical formula is not very intuitive, it’s hard for our mind to really wrap itself around the concept and really understand how compounding makes such a huge difference. I think a good way to get a feel for it is to play with some numbers on an online calculator like this one.
Let’s try and understand it more with some examples.
Example 1: Imagine you’re a fresh graduate from high school or college, and you’ve just landed your first job. You don’t have any investments yet (initial investment = $0), and while your income is modest, you’re committed to investing for your future. With hard work and discipline, you manage to save and invest $500 every month. Let’s assume you put that money into an index fund in the stock market that, on average, offers a 7% annual return.
For the sake of simplicity, let’s also assume that you continue saving and investing $500 a month consistently for the next 40 years. Based on these assumptions, the numbers would look something like this:
Over the course of 40 years, you would have contributed a total of $240,000 toward your investment. However, thanks to the power of compound interest, your investment would grow to an astounding $1,197,810.67—over a million dollars! Isn’t that incredible?
This simple scenario doesn’t account for the fact that you’ll likely advance in your career and increase your salary, which means your monthly savings could also grow over time. But even if you stick to just $500 a month, you’re still on track to become a millionaire.
Example 2: Now let’s assume you’re 30 years old and have been working for a few years, managing to save $50,000 for your future. You decide to invest this $50,000 in the stock market through an index fund, which gives an average return of 7% annually. If you invest this money and never add another dollar to it, allowing it to simply compound for 30 years, your investment would grow to $380,612.75 by the time you reach 60—around the typical retirement age.
But let’s say you’re good at managing your expenses and are able to save and add about $1,000 each month to this investment. In that case, your balance would grow to over $1.5 million by the time you reach 60, as illustrated in the graph below.
Example 3: Let’s say you learn about investing at the age of 40. You’ve saved $100,000, which you now want to invest for your retirement at age 60. You’re also able to contribute $2,000 per month toward this investment. By the time you reach 60, your investment will grow to about $1.3 million.
While $1.3 million is a solid amount for retirement, you’ll notice that it’s not as much as in the previous example, where the 30-year-old started with $50,000 and only contributed $1,000 per month. The key difference is the amount of time the money had to compound. The earlier you start, the greater the impact of compound interest.
If you’re learning about this later in life, don’t worry—you haven’t missed the boat. The best time to start investing is as early as possible, and today is always a good time to begin.
The best way to get a sense of how these numbers work is to experiment with them using this calculator or any of the many available online.
Rule of 72
The Rule of 72 is a simple way to estimate how compound interest will grow your money over time. Calculating future growth in your head can be challenging, but it becomes easier when you think of it in terms of how many times your money will double. The key here is that the doubling time remains consistent for a given interest rate.
For example, if you want to determine how much an initial investment of $5,000 will grow over 30 years, and your money doubles every 10 years, here’s what happens:
- After the first 10 years, $5,000 doubles to $10,000.
- In the next 10 years (i.e., at the 20-year mark), it doubles again to $20,000.
- After another 10 years (i.e., at the 30-year mark), it doubles one more time to $40,000.
So, an initial investment of $5,000 becomes $40,000 after 30 years if the doubling time is 10 years.
Doubling time gives you an intuitive way to understand compound interest, and the Rule of 72 helps you calculate it based on a rate of return. Simply divide 72 by the annual rate of return to find the number of years it will take to double your investment. This can be expressed as:

For example, if you get a rate of return of say 18% on an investment then by rule of 72 it will take 72 ÷ 18 = 4 years to double your money. In the examples above, I assumed a 7% rate of return, which gives a doubling time of approximately 10.3 years (72 ÷ 7 = 10.3), or roughly 10 years. This is typical for investment in a broad market Index fund.
Conclusion
Investing, compound interest, and understanding how time impacts your returns are essential for building long-term wealth. The Rule of 72 and tools like online calculators can help simplify the math. Whether you’re just starting your financial journey or already have savings, the key is to start investing as soon as possible to take full advantage of the power of compound interest.

